Metode beda hingga utk menyelesaikan persamaan differensial
Salah
satu cara utk menyelesaikan persamaan differential adalah dengan
menggunakan metode beda hingga atau yg lbh dikenal dgn finite difference
method. Metode ini menggunakan pendekatan ekspansi Taylor di titik
acuannya (x). Ada tiga jenis beda (difference) yg bisa kita gunakan utk
mencari nilai f(x+∆x). Ketiga jenis beda ini disebut forward difference,
backward difference, dan central difference. Supaya gak lupa,
penurunannya saya berikan di sini.
Forward difference
Utk forward difference, kita ingin
mencari nilai suatu fungsi jika independent variablenya digeser ke depan
(makanya namanya forward difference) sebesar ∆x. Sederhananya, jika
kita tahu f(x), maka berapakah f(x+∆x)? Ekspansi Taylor dituliskan sbb:
Secara umum, symbol ∂f/∂x*∆x menunjukkan
kemiringan (gradient) nilai fungsi f pada f(x) jika x digeser sebesar
∆x. Sementara symbol ∂2f/∂x2 menunjukkan lengkungan (curvature) dari titik f(x) tsb jika x digeser sebesar ∆x.
Oleh karena nilai setelah term pertama di atas tidak signifikan dibandingkan dgn term kedua, maka bisa kita bilang klo:
Hubungan di atas menunjukkan kemiringan (gradient) dari fungsi tsb sebesar ∆x ke depan (lbh besar dari x).
Backward difference
Pertanyaan yg sama jg kita berikan utk
backward difference. Jika kita tahu f(x), maka berapakah f(x-∆x)? Atau
berapakah nilai fungsi tsb jika independent variablenya digeser ke
belakang sebesar ∆x. Ekspansi Taylor dituliskan sbb:
Hubungan terakhir ini menunjukkan kemiringan (gradient) dari fungsi tsb sebesar ∆x ke belakang (lbh kecil dari x).
Central difference
Jenis bedar ketiga adalah beda tengah, di
mana kita akan mencari kemiringan dari fungsi tsb dgn menggunakan
perbedaan nilai fungsinya dari beda depan dan beda belakang. Secara
matematis, beda tengah adalah penjumlahan dari beda depan dan beda
belakang.
Second order derivation
Setelah pendekatan orde satu bisa kita
turunkan spt di atas, skrg kita bisa menurunkan persamaan utk pendekatan
orde dua. Penurunan di bawah ini saya mulai dari mengambil persamaan
orde satu dari beda depan (forward difference) yg mengandung penurunan
orde dua (second order differential). Fungsi ∂2f/∂x2 saya keluarkan, dan persamaan utk ∂f/∂x nya saya ambil dari pendekatan beda belakang (backward difference).
Dengan adanya dua pendekatan (orde satu dan orde dua) ini, kita bisa bekerja dgn contoh berikut:
Penyelesaian analitiknya adalah sbb:
Kondisi batas yg kita ketahui adalah sbb:
u pada r = 2 atau u(2) = 0.008
u(6.5) = 0.003
Yg ditanyakan adalah berapa nilai u di antara kedua nilai batas di atas.
Dengan metode beda hingga ini, kita akan
membuat node2. Katakanlah kita buat 4 node. Node yg pertama adalah saat
u(2), dan node yg keempat adalah u(6.5). 4 node yg kita pilih terdiri
atas 3 rentang, yakni rentang node 1-2, rentang node 2-3, dan rentang
node 3-4. Jarak rentang tsb adalah (6.5-2)/3 = 1.5. Maka, node 2 adalah
2+1.5 = 3.5. Node 3 adalah 3.5+1.5 =5. Yg skrg ingin kita ketahui
tentunya adalah nilai u pada saat r = 3.5 atau u(3.5) dan u(5).
Utk yg pertama ini, kita akan gunakan
pendekatan beda maju utk orde satu. Dengan memasukkan pendekatan yg udah
kita turunkan ke persamaan diferensial di atas, kita dapat:
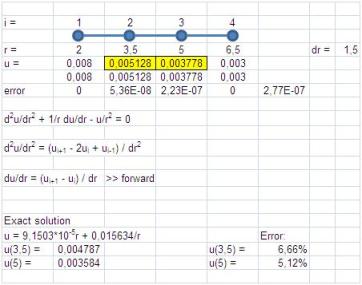
Persamaan ini kita utak-atik utk mendapatkan penyelesaian utk ui, sehingga kita bisa menyusun persamaan utk u2 dan u3. Sementara u1 dan u4 sudah kita ketahui sebagai kondisi batas. Klo saya selesaikan di excel, akan didapat sbb:
Perbandingan hasil pendekatan ini dengan hasil analitiknya menghasilkan error sebesar 6.66% utk u2 atau u(3.5) dan error sebesar 5.12% utk u3 atau u(5).
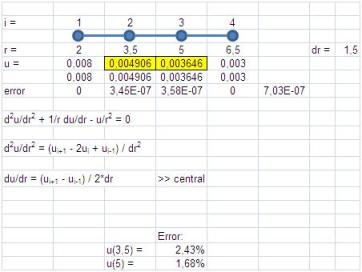
Jika saya gunakan beda tengah utk pendekatan orde satu, akan diperoleh hasil sbb:
Hasil perhitungan dgn pendekatan beda
tengah ternyata lbh akurat drpd pendekatan beda maju (dan jg drpd beda
mundur). Error utk u(3.5) menjadi 2.43% dan error utk u(5) menjadi
1.68%.
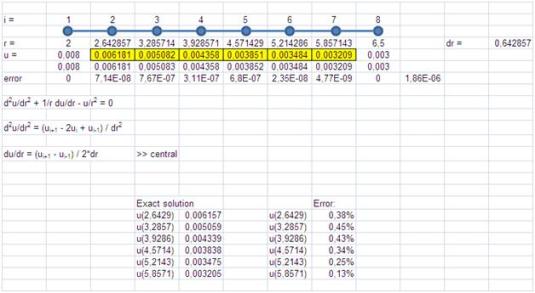
Jika saya menggunakan node yg lbh banyak,
dalam artian saya melakukan perhitungan yg lbh detail, dengan 8 node
misalnya. Dan tetap menggunakan beda tengah, akan didapat hasil sbb:
Spt yg diharapkan klo hasil perhitungan
dgn node yg semakin banyak atau perhitungan semakin detail, maka
hasilnya akan mendekati hasil analitiknya. Error yg diperoleh utk setiap
r di atas semuanya di bawah 0.5%.
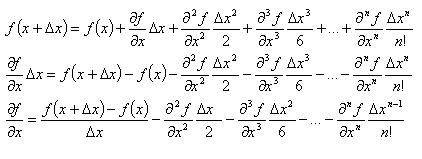
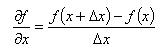
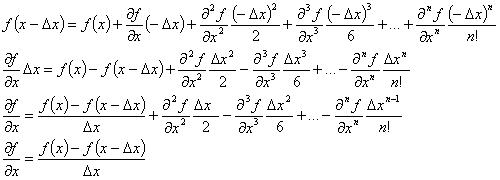
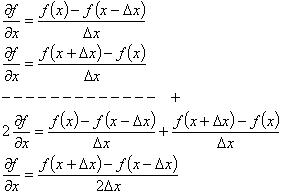
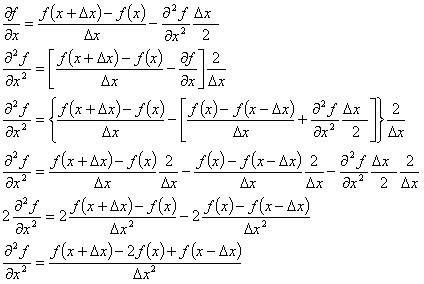
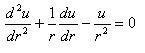
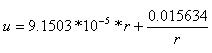
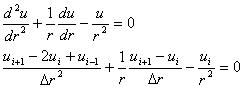
Komentar